前回の投稿でブロックチェーンの基本９ステップについて簡単に説明しました。
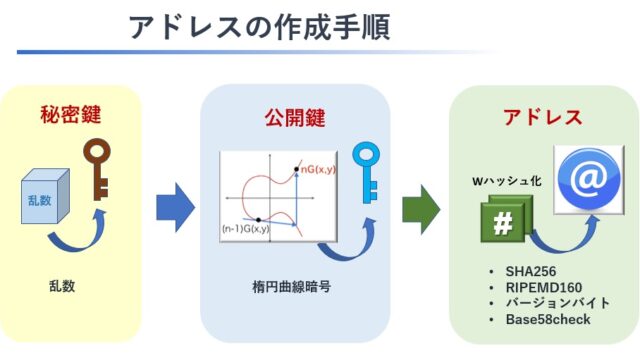
今回はその中の最初のステップであるアドレスの作成について、ソフトウエアロジックを中心になるべくわかりやすく説明していきます。
ブロックチェーンのアドレスとは、例えば、ビットコインなどの暗号資産を送金したり受取る際に使用されもので、銀行における「口座番号」に相当します。
（※）前回同様、資料は2020年～2021年に社内で行われたライトニングトークで使用したものを適宜流用します。
（※）説明は2008年「サトシ・ナカモト」が発表したビットコインに関する論文をベースに説明していきます。
ブロックチェーンアドレスとは
ブロックチェーンで使われる「アドレス」とは、例えば、ビットコインなどの暗号資産を送金したり受取る際に使用されもので、銀行における「口座番号」に相当します。
（以後、分かりやすさから「暗号資産」のかわりに「仮想通貨」を使用します）
ただし、銀行の口座番号と最も違う点は、ブロックチェーンの情報はアドレスを含めた全ての取引履歴が公開されているという点です。
そのため、特定の個人とアドレスが固定化してしまうと個人情報やセキュリティ上のリスクがあるため、以下の特徴を備えてます。
- 通常、１か3から始まる27文字から34文字の英数字で構成
- 秘密鍵⇒公開鍵⇒アドレスの手順で簡単に何度も生成可能
- ダイナミックに変更しても取引に問題ない仕組み
例えばビットコインアドレスはこのような長い文字列から構成されます。
1EHNa6Q4Jz2yxYExL123mE43ikXhwF6kZm
ビットコインアドレスの種類
ビットコインアドレスは１か3から始まると説明しましたが、実際にはいくつか種類がありますので簡単に紹介しておきます。
- 「1」から始まるアドレス（秘密鍵による署名が一つ）
- 「3」から始まるアドレス（秘密鍵による署名が複数）
- 「bc1」から始まるアドレス（Segwitに対応したアドレス）
- 「m」「n」から始まるアドレス（開発用/テストネット）
※）「Segwit」とはデータ圧縮とトランザクション展性（ID書換容易性）対策のためにとられた手法です（別稿参照）
アドレスの基礎知識
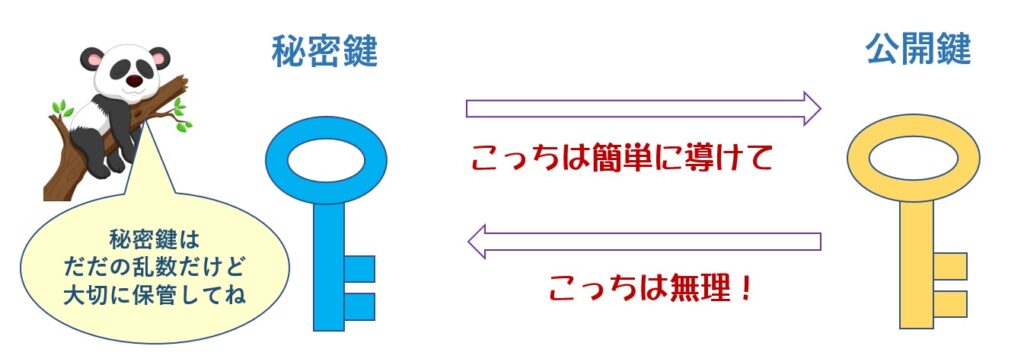
秘密鍵とは
秘密鍵とは、鍵ペアのうち自分だけが知っている鍵で、自分自身を証明する手段となります。
ビットコインの場合、秘密鍵は一般的に2の256乗（十進数だと78桁）と、とても大きな範囲の数字ですが、コンピュータでは疑似乱数として簡単に生成することができます。
秘密鍵は、公開鍵、ビットコインアドレス、トランザクション、等の生成時に使われるため、これが第三者に知られてしまうと自分の仮想通貨が自由に使われてしまうことになります。
公開鍵とは
公開鍵は、鍵ペアのうち自分自身の証明のために他者に公開するための鍵で、ビットコインの場合、仮想通貨の送金先を指定したり、トランザクションの正当性を電子署名で確認するときなどに使用します。
秘密鍵は楕円曲線暗号技術を使用して機械的に公開鍵を生成することができます（後述）
逆に公開鍵から秘密鍵を数学的に特定するのは、現実的に不可能だと言われています。
（図）秘密鍵と公開鍵（画像をクリックで拡大）
離散対数問題
上記のような関係の事をことを離散対数問題（discrete logarithm problem）と呼んでます。
例えば素数同士の掛け算で考えてみましょう。
95,461 X 54,787 = 5,230,021,807
この式で左から右への掛け算は簡単に求まりますが、逆に結果の5,230,021,807から2つの素数を導き出すのはちょっと苦労しそうですね。
これが離散対数問題の特徴です。
ビットコインで使われる楕円曲線暗号
ビットコインでは秘密鍵から公開鍵を生成するために楕円曲線暗号が使用されます。
一般的な数式は以下のとおりです。
剰余演算modについて
modは言わずと知れた剰余演算（割算をした時の余り）で、ここでも離散対数問題の性質が利用されてます。
例えば、一般的にy=ax mod pの場合、xからyを求めるのは簡単ですが、yからxを求めるのは桁数が大きくなればなるほど難しくなりますね。
結局そのグラフは楕円ではなく以下のようなタコを横に寝かしたようなグラフとなります。
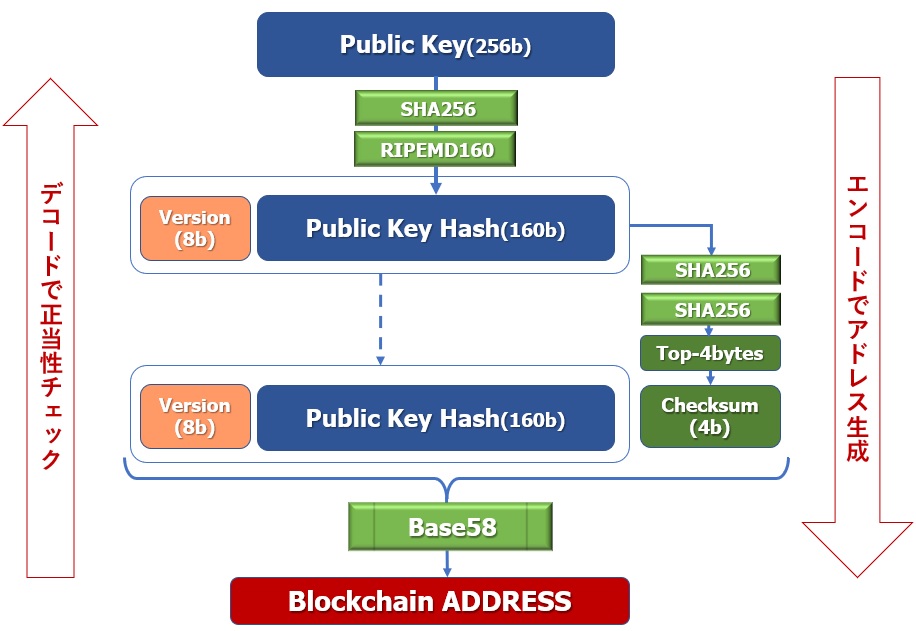
Version byteについて
上記の図にオレンジ色のVersion(8b)というのがありますが、これはバージョンバイト、あるいはバージョンプリフィックスと呼ばれ、生成するアドレスのタイプを表してます。
以下にバージョンバイトの一例を示します。
- 0x00:公開鍵ハッシュ
- 0x05:スクリプトハッシュ
- 0x80:秘密鍵WIF形式
※）詳細はこちらのサイトを参照して下さい。
秘密鍵から公開鍵の生成方法
Blockchain Bizによると実際に楕円曲線暗号で公開鍵を求める手順は以下のようになるようです。
（出典：Blockchain Biz）
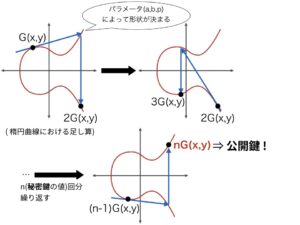
- 基準点G(x,y)に
- G(x､y)＋ G(x､y)＝２Ｇを求める
- ②をn回（n:秘密鍵)分繰返して
（このnが2の245乗） - nGを公開鍵とする
ここを詳細に調査しだすと暗号と数学の極みにはまっていくので我々ソフトウエアエンジニアとしてはライブラリを有効に使っていきましょう。
公開鍵をソフトウエア的に導く
ここではプログラムでロジックを明確にすることが目的ですので言語は何でもよいのですが、分かりやすさという点からPhythonを使用することにします。
（開発環境はAnacondaのJupyper notebook）
公開鍵生成に関してポイントとなるのが、楕円曲線暗号Secp256k1をどのように実装するかなんですが、実はPhtyonにはサードパーティ製のライブラリであるecdsa（※）という優れものがあるので、早速インストールして利用することにしました。
まず秘密鍵は標準ライブラリのos.urandomを使用しprivate_keyを生成します。
それをライブラリecdsaのマニアル通りに引き数private_keyを設定すると一瞬にしてpublic_keyを生成することができました。
※）ecdsaはelliptic curve digital signature algorithmの略です。
プログラム
import os
import binascii
import ecdsa
# create private key from randam function
private_key = os.urandom(32)
# generate public_key used by SECP256k1
public_key = ecdsa.SigningKey.from_string(private_key,
curve=ecdsa.SECP256k1).verifying_key.to_string()
#output private and public key
print( “private key=”,binascii.hexlify(private_key) )
print( “public key=”,binascii.hexlify(public_key) )
結果
private key= b’8979a2f611f9d2afb410d92442257d30213e958e1b6db0
196b4766c99dba4bf8′
public key= b’6f9db274ce933de283df0093bf1e093ffa046830da8fb7a8
ae7bb5b3178f06720f30fc0319d1f27d5d5ce892384ae650f48c3d6894e
d8680ce135f4f876734cd’
このようにライブラリを使用すれば、楕円曲線暗号の難しい勉強は不要となります。
ecdsaを作成したサードパーティさんに感謝ですね。
圧縮型の公開鍵とは
既に説明している通り公開鍵は楕円曲線暗号を利用して生成されるので、その結果は座標となります。
その結果、秘密鍵は256bitですが、公開鍵はその2倍のサイズとなり、前半がx座標、後半がy座標です。
ブロックチェーンでは、スケーラビリティの向上のために、１MBのブロックの中になるべく多くのトランザクションを組み込みたい、つまり１つのトランザクションのデータサイズをいかに小さくするというのが重要なテーマの一つになってます。
※）前述のsegwitもその手法の一つで、トランザクションのINPUT領域に記録されているscriptSig（INPUTの約60%に相当）をブロック外のwitnessという領域に保存してます。
そこで、公開鍵が楕円曲線上の座標であることを利用すればx座標の情報だけでy座標を導くことが可能だということで、上記の数字をそのまま使う非圧縮型とx座標のみで構成する圧縮型の公開鍵フォーマットが生まれました。
非圧縮の場合には上記で導出された公開鍵の先頭に04というプレフィックスを付加し、圧縮の場合には、x座標から導いたy座標が正の場合（座標値が偶数）には02、負の場合（座標値が奇数）には03を付加することになってます。
（図）非圧縮型と圧縮型の公開鍵フォーマット
ビットコインアドレスとは
これまで、乱数により生成した秘密鍵、それを楕円曲線暗号を使用して公開鍵を作成するまでを説明しました。
そして秘密鍵が漏洩しないよう大切に保管する限り、関係者に配布する公開鍵から秘密鍵の導出は事実上不可能であることも分かりましたね。
それでは公開鍵自体をアドレスにしてはどうでしょうか？
上記で計算した公開鍵をもう一度見てみましょう。
b’6f9db274ce933de283df0093bf1e093ffa046830da8fb7a8ae7bb5b3178f06720f30fc0319d1f27d5d5ce892384ae650f48c3d6894ed’
圧縮方式にしたとしてもこの半分の長さであり、実用上ちょっとハンドリングが悪いそうです。
そのためビットコインでは公開鍵に対して以下の3つの対策をとったものをアドレスにしてます。
- ハッシュ化して短縮する（sha256とRIPEMD160）
- チェックサムを組み込み記入ミスを検出しやすくする
- 可読性を向上するためBase58でエンコードをする
アドレスを生成するときに使用するハッシュ関数はsha256とRIPEMD160を使用し、160ビット（16進数だと40桁）の数字を生成します（2種類のハッシュ関数を利用しているので以後これを”Wハッシュ”と表記します）
※）sha256は「シャニゴロ」「シャアニゴロ」、RIPEMDは「リップエムド」、「ライプエムディー」等と呼ばれてます。
以下にアドレスの作成手順をまとめておきます。
BASE58
皆さんはBASE64というのはなじみがあるともいます。
主にeメールに添付する画像や音声などのバイナリデータはそのままでは送信できませんので文字列に変換する必要がありますが、その際8ビットから6ビット（64文字）にエンコードすることによりデータ量を四分の三にできるというものでした。
ブロックチェーンのアドレスにする場合にはeメールに加えて可読税を向上し、読み間違えなどない文字列を使用する必要がありました。
そのためBASE64に対して以下の6個の文字列を使用しないようエンコードしています。
- 「+」（プラス）
- 「/」（スラッシュ）
- 「0」（数字のゼロ）
- 「O」（アルファベットoの大文字）
- 「I」（アルファベットiの大文字）
- 「l」（アルファベットLの小文字）
Base58Check
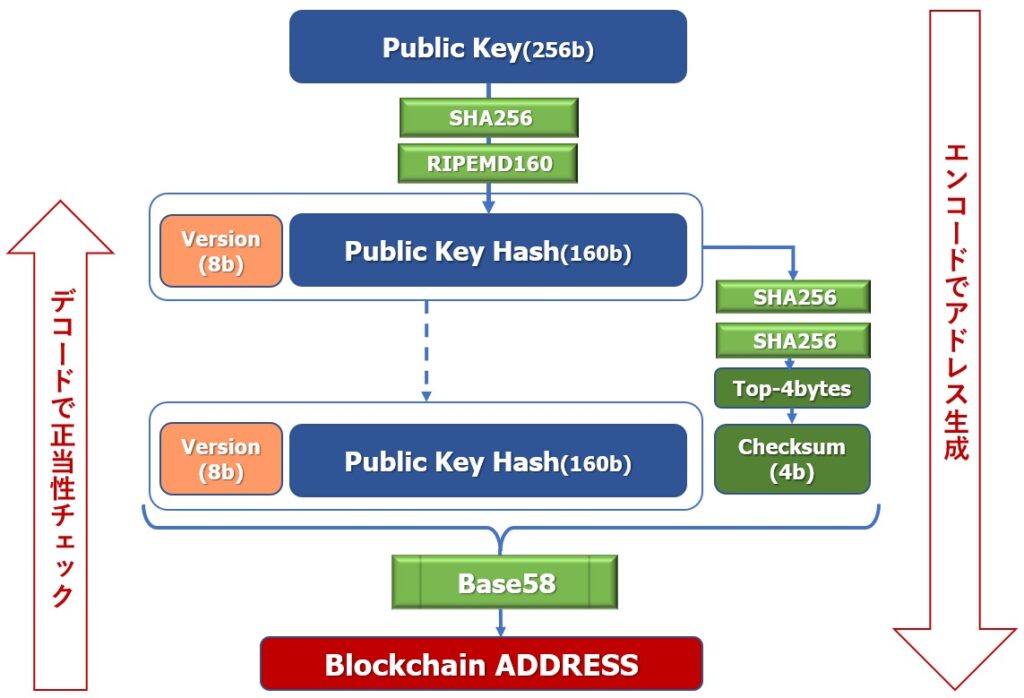
公開鍵をsha256とRIPEMD160でWハッシュ化し、BASE58でエンコードした後、更にデータの正当性を確認するためにチェックサムを組み込みアドレスを生成します。
チェックサムは、公開鍵をハッシュ化してその先頭にバージョンバイトを付加した値をsha256で2回ハッシュ化した数値の先頭4バイトです。
以下にBase58Checkのエンコードの手順をまとめておきます。
（図）Base58Checkのプロセス
アドレスを生成してみよう
以上の説明から早速プログラムで公開鍵からアドレスを生成してみましょう。
以下の手順でしたね。
- ハッシュ化して短縮する（sha256とRIPEMD160）
- チェックサムを組み込み記入ミスを検出しやすくする
- 可読性を向上するためBase58でエンコードをする
この手順をもとに、上記のフローチャート（図 Base58Checkのエンコードの手順）に従い作成したプログラムとその結果を掲載しておきます。
逐一コメントを入れ、都度結果も出力しているので、皆さんなら読めばわかると思いますので説明は省略します。
これをコピペしてJupter Notebookで実行してみてください。
最初の乱数発生の値が実行の都度異なりますので、毎回異なったアドレスが生成されるのが分かります。
プログラム
import os
import ecdsa
import hashlib
import base58
import binascii
# generate public key form private key
private_key = os.urandom(32)
public_key = ecdsa.SigningKey.from_string( private_key, curve=ecdsa.SECP256k1 ).verifying_key.to_string()
print( “*public key=”, binascii.hexlify( public_key) )
# add prefix(0x04) as “uncompressed public key”
prefix_and_pubkey = b”\x04″ + public_key
print( “*prefix and public key=”, binascii.hexlify(prefix_and_pubkey) )
# generate 160-bit hash by double hash(sha256 and ripemd160)
ripemd160 = hashlib.new( ‘ripemd160’ )
ripemd160.update( hashlib.sha256( prefix_and_pubkey ).digest() )
hash160 = ripemd160.digest()
print( “*hash160=”, binascii.hexlify( hash160 ) )
# add version byte (0x00) : means “pubkey_hash”
pubkey_hash = b”\x00″ + hash160
# hash pubkey_hash two times with sha256
double_sha256 = hashlib.sha256( hashlib.sha256( pubkey_hash ).digest() ).digest()
print( “*double hash key=”, binascii.hexlify( double_sha256 ) )
# extract 4 bytes-checksum from the top of double_sha256
checksum = double_sha256[:4]
# add checksum to the bottom of row address
row_address = pubkey_hash + checksum
print( “*row address( before base58 )=”,binascii.hexlify( row_address ))
# create blockchain address by base58 encoding
address = base58.b58encode( row_address )
print( “*blockchain address=”,address.decode() )
結果
*public key= b’e9ed1d04ce560dd14687d60216ca6d17e0fa3febb044bb94c78c33f9657e829ace23aa11b163ce773b01bd93c9a6b08047356be7d2ade8d9f45c05b2ba7f17cd’ *prefix and public key= b’04e9ed1d04ce560dd14687d60216ca6d17e0fa3febb044bb94c78c33f9657e829ace23aa11b163ce773b01bd93c9a6b08047356be7d2ade8d9f45c05b2ba7f17cd’ *hash160= b’5fc29f9913ad60c72ca052f1c3333058c2c052e5′ *double hash key= b’f1a0c94dc3e78957e142fde501d0dda719f2f26012d33a4afb1264d251793ebe’ *row address(before base58)= b’005fc29f9913ad60c72ca052f1c3333058c2c052e5f1a0c94d’ *blockchain address= 19jLLu1yU3ciAJfEcvNmnRxD3QbPsLMjFi
実際にアドレスを確認してみよう
それではスマホにウォレットアプリSafePalをインストールして、実際にCoinchekという取引所に送金するデモンストレーションをご覧ください。
これは弊社のライトニングトークALT(Arp Lightning Talk）で使用した映像ですが、今回公開するにあたり、ドレスやトランザクションIDの一部にぼかしを入れてます。
多少お見苦しい点はあるかと思いますが、雰囲気はお分かりいただけると思います。
以上
ケニー狩野（中小企業診断士、PMP、ITコーディネータ）
キヤノン(株)でアーキテクト、プロマネとして多数のプロジェクトをリード。
現在、株式会社ベーネテック代表、株式会社アープ取締役、一般社団法人Society 5.0振興協会評議員ブロックチェーン導入評価委員長。
これまでの知見を活かしブロックチェーンや人工知能技術の推進に従事。趣味はダイビングと囲碁。
２０１８年「リアル・イノベーション・マインド」を出版。
第２回：ブロックチェーンとは
